12.1 What is a binary search tree?
12.1-1¶
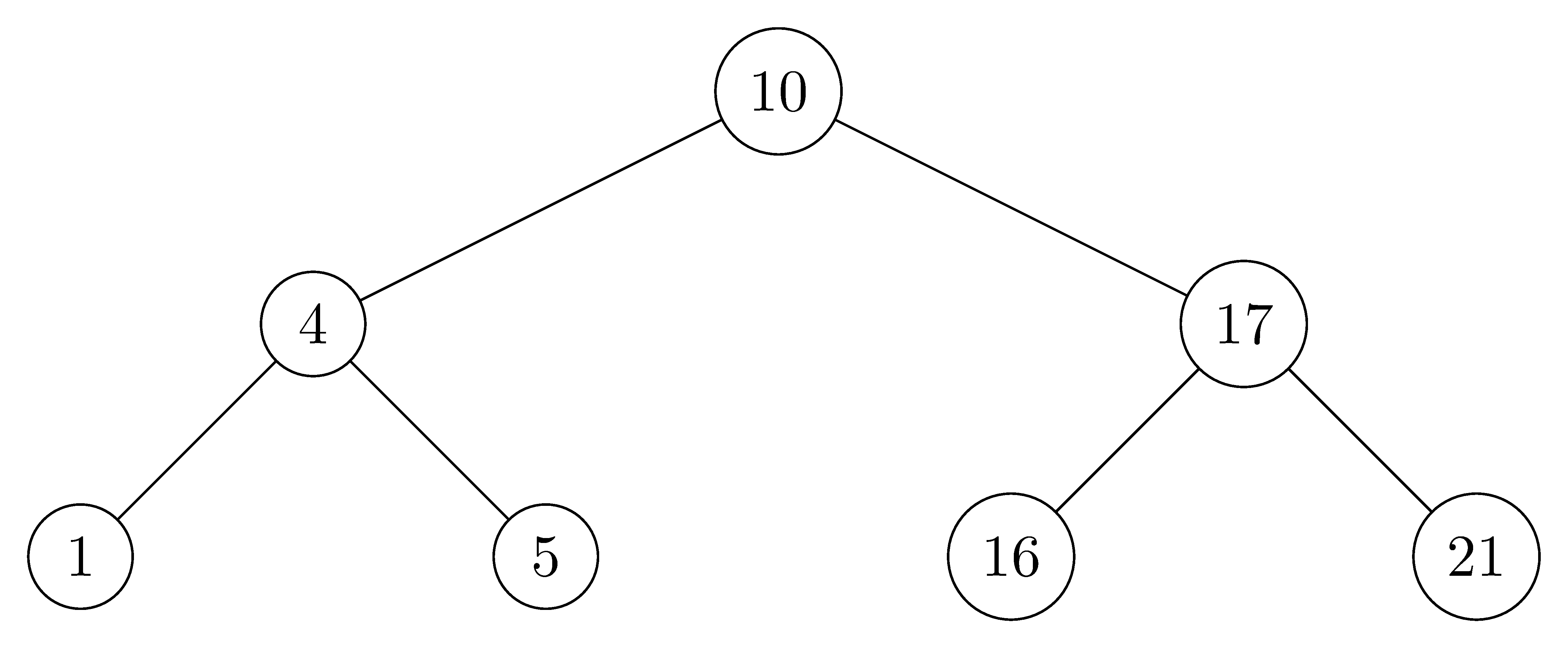
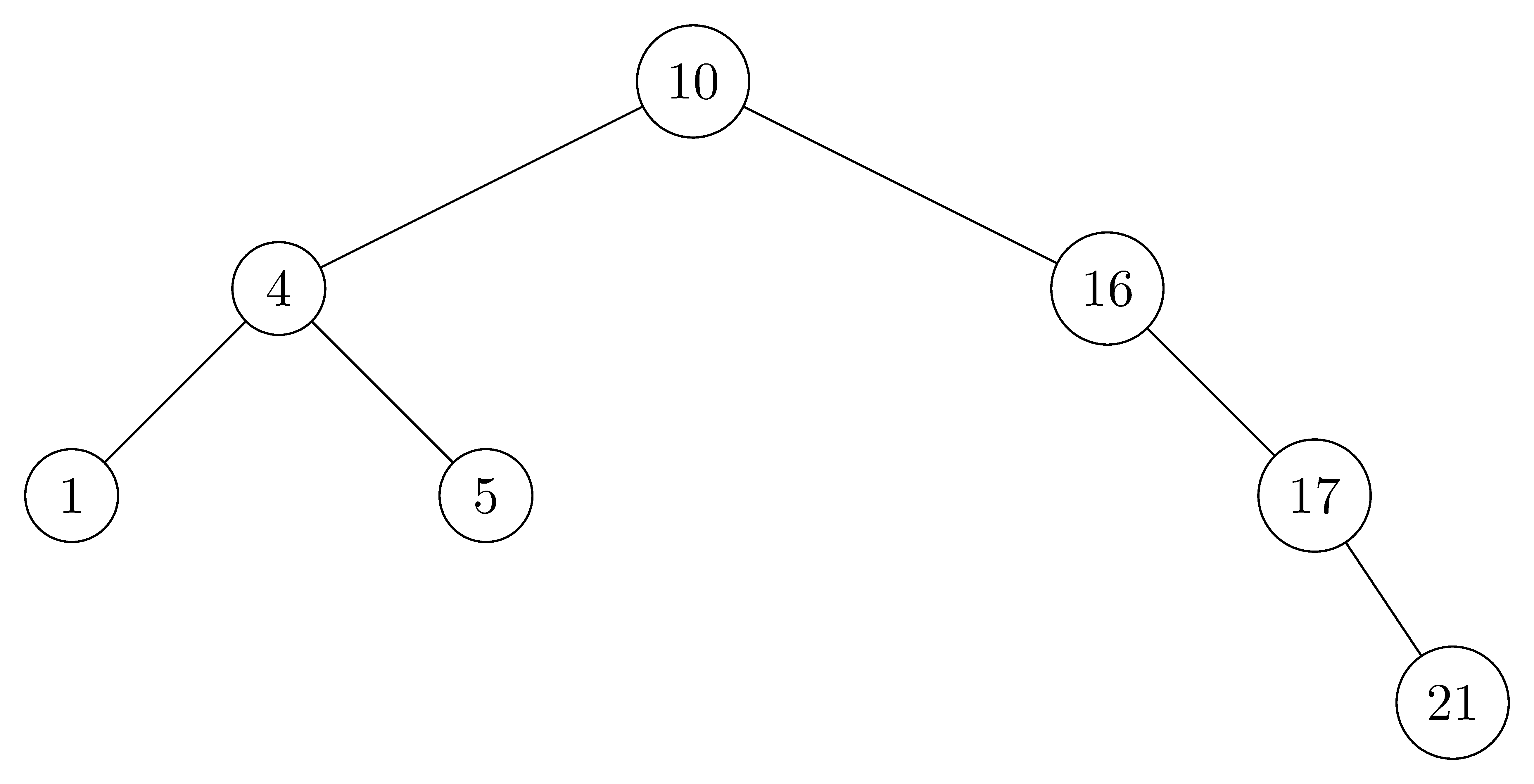
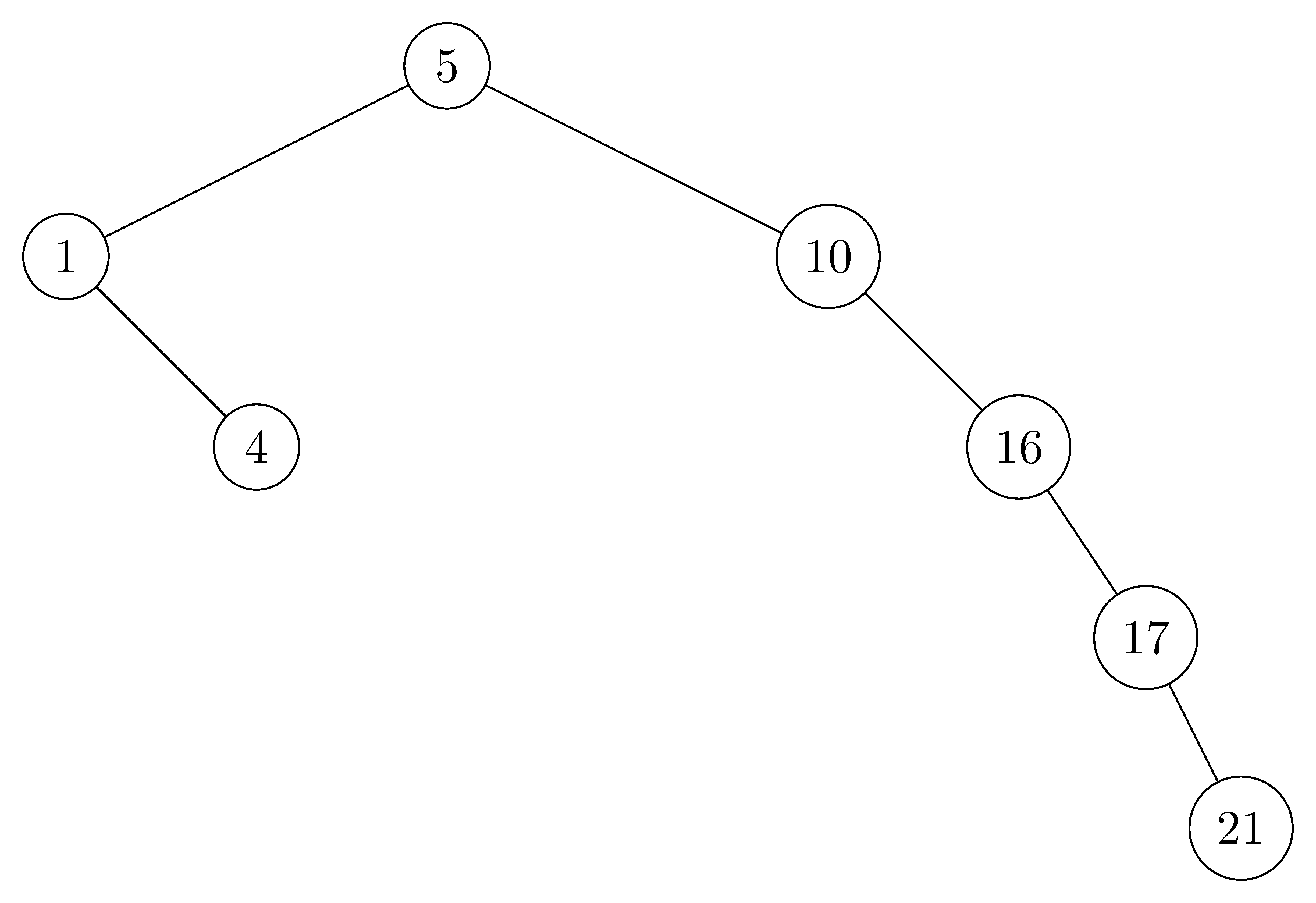
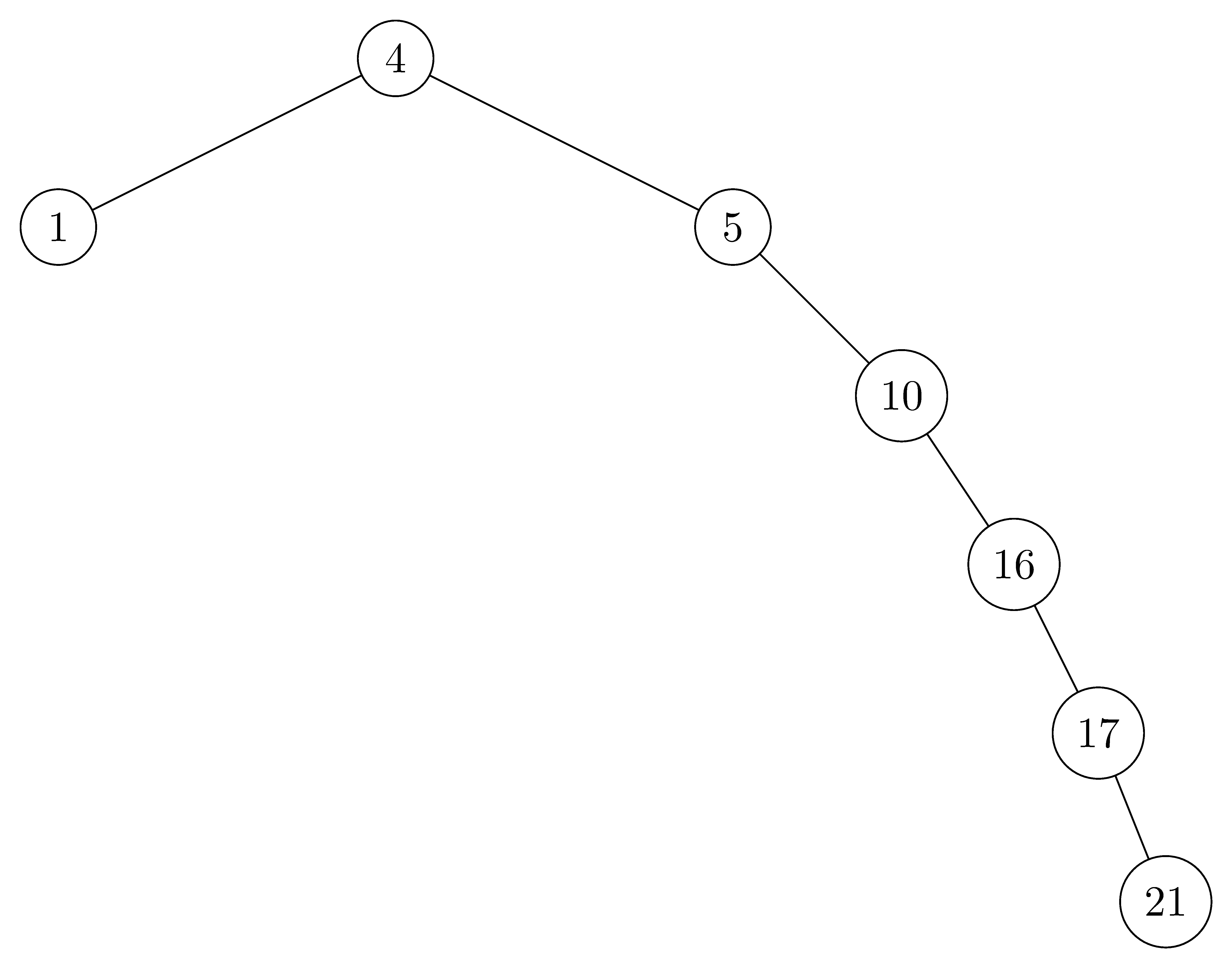
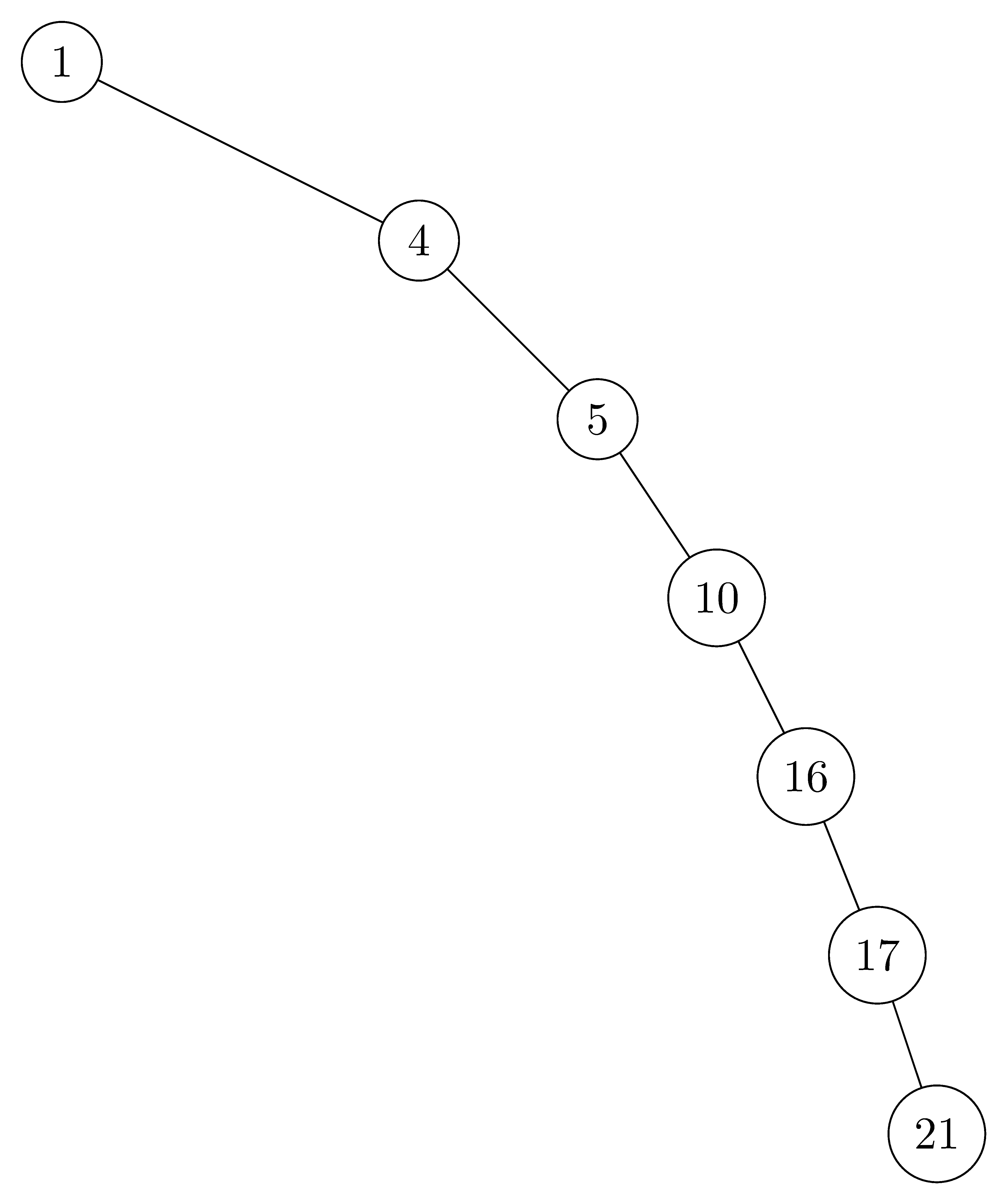
For the set of $\{ 1, 4, 5, 10, 16, 17, 21 \}$ of keys, draw binary search trees of heights $2$, $3$, $4$, $5$, and $6$.
- $height = 2$:
- $height = 3$:
- $height = 4$:
- $height = 5$:
- $height = 6$:
12.1-2¶
What is the difference between the binary-search-tree property and the min-heap property (see page 153)? Can the min-heap property be used to print out the keys of an $n$-node tree in sorted order in $O(n)$ time? Show how, or explain why not.
- The binary-search-tree property guarantees that all nodes in the left subtree are smaller, and all nodes in the right subtree are larger.
- The min-heap property only guarantees the general child-larger-than-parent relation, but doesn't distinguish between left and right children. For this reason, the min-heap property can't be used to print out the keys in sorted order in linear time because we have no way of knowing which subtree contains the next smallest element.
12.1-3¶
Give a nonrecursive algorithm that performs an inorder tree walk. ($\textit{Hint:}$ An easy solution uses a stack as an auxiliary data structure. A more complicated, but elegant, solution uses no stack but assumes that we can test two pointers for equality.)
INORDER-TREE-WALK(T)
let S be an empty stack
current = T.root
done = 0
while !done
if current != NIL
PUSH(S, current)
current = current.left
else
if !S.EMPTY()
current = POP(S)
print current
current = current.right
else done = 1
12.1-4¶
Give recursive algorithms that perform preorder and postorder tree walks in $\Theta(n)$ time on a tree of $n$ nodes.
PREORDER-TREE-WALK(x)
if x != NIL
print x.key
PREORDER-TREE-WALK(x.left)
PREORDER-TREE-WALK(x.right)
POSTORDER-TREE-WALK(x)
if x != NIL
POSTORDER-TREE-WALK(x.left)
POSTORDER-TREE-WALK(x.right)
print x.key
12.1-5¶
Argue that since sorting $n$ elements takes $\Omega(n\lg n)$ time in the worst case in the comparison model, any comparison-based algorithm for constructing a binary search tree from an arbitrary list of $n$ elements takes $\Omega(n\lg n)$ time in the worst case.
Assume, for the sake of contradiction, that we can construct the binary search tree by comparison-based algorithm using less than $\Omega(n\lg n)$ time, since the inorder tree walk is $\Theta(n)$, then we can get the sorted elements in less than $\Omega(n\lg n)$ time, which contradicts the fact that sorting $n$ elements takes $\Omega(n\lg n)$ time in the worst case.